LeetCode Hard – Largest Rectangle in Histogram

Given an array of integers heights representing the histogram’s bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.

Example 1:

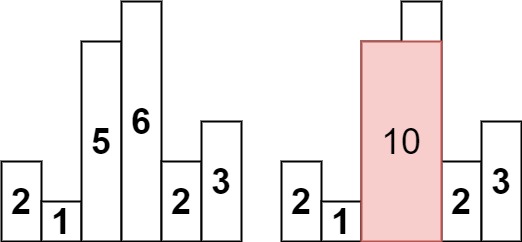
Input: heights = [2,1,5,6,2,3]

Output: 10

Explanation: The above is a histogram where width of each bar is 1. The largest rectangle is shown in the red area, which has an area = 10 units.

Example 2:

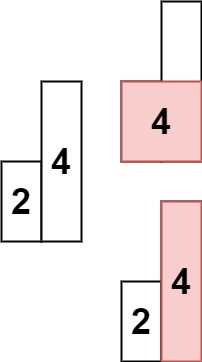
Input: heights = [2,4]

Output: 4

Constraints:

• 1 <= heights.length <= 105
• 0 <= heights[i] <= 104

Java Solution

You can solve this problem using a stack to efficiently find the maximum area of a rectangle in the histogram. Here’s the Java code for the solution:

import java.util.Stack;

public class LargestRectangleInHistogram {
    public static int largestRectangleArea(int[] heights) {
        Stack<Integer> stack = new Stack<>();
        int maxArea = 0;

        for (int i = 0; i <= heights.length; i++) {
            int currentHeight = (i == heights.length) ? 0 : heights[i];

            while (!stack.isEmpty() && currentHeight < heights[stack.peek()]) {
                int height = heights[stack.pop()];
                int width = stack.isEmpty() ? i : i - stack.peek() - 1;
                maxArea = Math.max(maxArea, height * width);
            }

            stack.push(i);
        }

        return maxArea;
    }

    public static void main(String[] args) {
        int[] heights1 = {2, 1, 5, 6, 2, 3};
        System.out.println(largestRectangleArea(heights1));  // Output: 10

        int[] heights2 = {2, 4};
        System.out.println(largestRectangleArea(heights2));  // Output: 4
    }
}

This Java code defines a largestRectangleArea method that takes an array of histogram heights as input and returns the area of the largest rectangle. The algorithm uses a stack to keep track of the indices of the histogram bars. It iterates through the heights, calculating the maximum area by popping elements from the stack when the current height is less than the height at the top of the stack. The final result is the maximum area of the rectangle in the histogram. The provided test cases demonstrate its usage.

Python Solution

def largestRectangleArea(heights):
    stack = []
    maxArea = 0

    for i in range(len(heights) + 1):
        currentHeight = 0 if i == len(heights) else heights[i]

        while stack and currentHeight < heights[stack[-1]]:
            height = heights[stack.pop()]
            width = i if not stack else i - stack[-1] - 1
            maxArea = max(maxArea, height * width)

        stack.append(i)

    return maxArea

# Test cases
heights1 = [2, 1, 5, 6, 2, 3]
print(largestRectangleArea(heights1))  # Output: 10

heights2 = [2, 4]
print(largestRectangleArea(heights2))  # Output: 4

This Python code uses a similar approach with a stack to efficiently find the maximum area of a rectangle in the histogram. The largestRectangleArea function takes an array of histogram heights as input and returns the area of the largest rectangle. The provided test cases demonstrate its usage.